여기저기 논문에서 나오는 개념에 대해서 한번 정리하고자 합니다.
선형대수 수업을 들을때 이런 내용이 있었는지 기억이 안나서 열심히 공부해둘걸 후회중입니다.
인공지능을 통해서 얻은 지식또한 존재하므로 틀린 부분은 지적 부탁드립니다
전체 요약




사실 저는 저기까지만 보면 그래서 저게 어디에 쓰이는데 라는 생각과 예시가 없다는 생각이 먼저 들어서 이해가 잘 안되곤 합니다. (공돌이의 숙명인걸까요)
하나씩 자세히 뜯어보겠습니다
Gradient, 그래디언트, ∇f
스칼라 값 함수 f의 모든 편미분을 원소로 가지는 벡터입니다.
쉽게 말해서 함수 f의 입력 변수가 여러 개일 때, 각 변수에 대해서 얼마나 영향을 받는지 변화율(기울기)를 모아둔 벡터라고 보시면 됩니다.

인공지능이 뜨면서 경사하강법, Gradient Descent 에 자주 나오는 그 녀석입니다. 최적화 과정을 수행하면서 특정 지점에서의 gradient를 구하면 가장 값이 빠르게 증가하는 벡터를 얻을 수 있는데요, 여기에 -1을 곱하면 가장 빠르게 내려가는 벡터를 얻을 수 있겠죠. 이를 통해서 다음 단계로 이동할 방향을 결정하기 위해 gradient가 연산되어 사용됩니다.
예시 함수
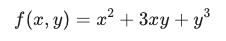
계산된 Gradient

Jacobian, 자코비안, 야코비안, J
스칼라 값을 뱉는 함수가 아닌, 벡터 값을 뱉는 함수의 1차 편미분을 모아둔 행렬입니다.
위의 그래디언트가 스칼라 함수의 편미분을 모아둔 벡터였다면 자코비안은 여러개의 함수의 편미분을 모아둔 행렬이라고 생각하시면 됩니다. (실제로 결과 벡터의 차원이 1인 경우 자코비안은 그래디언트의 전치와 같습니다)

그래디언트가 여러 변수에 의해 영향을 받는(다변수) 스칼라 값에서 가장 가파른 상승 방향(미분)을 알려주었다면,
자코비안은 여러 변수에 의해 영향을 받는(다변수) 벡터 값 함수의 미분을 나타내는 행렬입니다.
그렇기에 자코비안 행렬은 특정 지점에서 각 변수가 조금씩 변화할때(dx) 최종적으로 함수 값의 출력에 어떤 변화를 가져오는지 보여줍니다.
좀 더 수학적으로 멋있게 표현하면 국소 지점에서의 선형 변환을 근사시킬 수 있습니다.

비선형 변환의 선형변환 근사 이미지는 아래 링크에서 확인하실 수 있습니다
https://angeloyeo.github.io/2020/07/24/Jacobian.html
(행렬 곱, 선형 변환은 한 공간에서 다른 공간으로의 사상, map 이라는 관점을 가지고 있으면 좀 더 직관적으로 이해할 수 있습니다)
이때 이 자코비안 행렬의 행렬식, determinant를 구하면 이 선형 변환을 통해 미소 부피가 얼마나 크게 변하는지 그 변화율을 알아낼 수 있습니다.
예시 함수
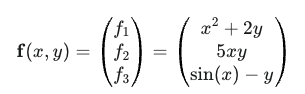
계산된 자코비안

Hessian, 헤시안, 헤세, H
헤시안 행렬은 다변수 스칼라 값 함수의 2차 편미분을 원소로 가지는 정사각 행렬입니다.

그래디언트(벡터)를 다시 한번 입력 변수에 대해서 미분한 결과(=자코비안) 이라고 보셔도 됩니다.

헤시안 행렬은 클레로의 정리(Clairuat's Theorem)이 적용되는데요, 간단하게 표현하자면 대칭 행렬이라는 의미입니다
클레로의 정리(Clairuat's Theorem)
함수와 그 2차 편미분들이 연속적이라고 가정하면 편미분의 순서는 결과에 영향을 끼치지 않습니다.
행렬에서의 비대각 성분들이 주대각선을 기준으로 서로 순서만 바뀐 형태이기에 대칭행렬이라는 사실을 유도할 수 있습니다.
그래서 이 헤시안 행렬은 기하학적으로 어떤 의미가 있을까요?
이 함수는 2차 미분을 모아둔 행렬이기에 함수의 곡률, Curvature을 의미합니다. 얼마나 볼록한지(Convexity), 오목한지(Concavity)를 그 크기와 방향을 알려주는 행렬이라고 볼 수 있습니다.
그래디언트가 0인 지점 (평평한 지점)에서 헤시안 행렬의 고윳값(Eigenvalue)를 구하고 이 부호를 확인해보면 함수의 모양을 알 수 있습니다.
- 모든 고윳값이 양수: 해당 지점은 지역 최소값(Local Minimum)입니다
- 모든 고윳값이 음수: 해당 지점은 지역 최대값(Local Maximum)입니다
- 양수와 음수가 섞여 있음: 해당 지점은 안장점(Saddle Point)입니다.

이 헤시안 행렬은 최적화 - Newton's Method에서 주로 사용된다고 합니다.
예시 함수

계산 결과

대칭행렬임을 보실 수 있습니다.
Laplacian, 라플라시안, Δf 또는 ∇^2f
라플라시안은 스칼라 함수 f의 그래디언트의 발산(Divergence)입니다. 다르게 말해서 2차 편미분의 합이라고도 표현할 수 있겠습니다.

이 라플라시안 값은 헤시안 행렬 H의 대각합(Trace)와 같은 것을 알 수 있습니다.

이 라플라시안은 특정 지점에서의 평균 곡률과 관련이 있는데요, 해당 곡률의 합이 0보다 크다면 해당 지점은 오목한 경향이 있습니다. 반대라면 볼록한 경향이 있구요. (어렸을때 배운 2차함수의 최고차항 부호에 따라 아래로 오목한지, 위로 볼록한지를 생각해보시면 좋습니다).
이를 메시같은 이산공간에서
예시 함수 (헤시안과 동일)

결과
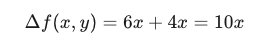
헤시안 행렬의 대각합과 같은 결과가 나옴을 보실 수 있습니다.
이렇게 그래디언트, 자코비안, 헤시안, 라플라시안에 대해서 정리가 끝났습니다.
언제쯤이면 막히는 부분 없이 논문을 읽을 수 있을지 걱정되지만 꾸준히 공부하다보면 그런 날이 올거라 믿고 열심히 하는 수 밖에 없겠습니다.
참고자료
[Optimization] 그래디언트(Gradient), 헤시안(Hessian), 자코비안(Jacobian) 개념 정리
Gradient, Hessian, Jacobian matrix 최적화에서 중요한 개념인 Gradient, Hessian, Jacobian에 대해 알아보겠습니다. 그 전에 함수의 미분 가능성과 연속성에 대해 기억이 잘 나시지 않는다면 이전 글을 참고해
exvarx.tistory.com
https://darkpgmr.tistory.com/132
Gradient, Jacobian 행렬, Hessian 행렬, Laplacian
Gradient(그레디언트), Jacobian(야코비언) 행렬, Hessian(헤시안) 행렬, Laplacian(라플라시안) ... 문득 정리의 필요성을 느껴서 적어봅니다. 이들을 함께 보는 이유는? 그냥 왠지 이들은 세트로 함께 봐야
darkpgmr.tistory.com
https://gaussian37.github.io/math-calculus-jacobian/
Gradient (그래디언트), Jacobian (자코비안) 및 Hessian (헤시안)
gaussian37's blog
gaussian37.github.io
https://angeloyeo.github.io/2020/07/24/Jacobian.html
자코비안(Jacobian) 행렬의 기하학적 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
https://angeloyeo.github.io/2020/06/17/Hessian.html
헤세 행렬(Hessian Matrix)의 기하학적 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
'연구' 카테고리의 다른 글
| MHR (Momentum Human Rig) 파라미터 및 Joint Hierarchy (0) | 2025.12.18 |
|---|---|
| [논문리뷰] SMEAR: Stylized Motion Exaggeration with ARt-direction (0) | 2025.11.26 |
| [논문리뷰] Text-to-Any-Skeleton Motion Generation Without Retargeting (0) | 2025.11.25 |
| [논문리뷰] DisCoRD: Discrete Tokens to Continuous Motion via Rectified Flow Decoding (0) | 2025.11.03 |
| [논문리뷰] Mean Value Coordinates for Closed Triangular Meshes (0) | 2025.10.23 |
